正六角形 (正6角形)の角度の求め方は? 内角の和、外角 正六角形 (正6角形)の1つの角度は1°です。 正六角形 (正6角形)の内角の和は、 180°× (n-2) =180°× (6-2) =180°×4=7° です。 正六角形の6つの角度は全て等しいので、7°を6で割れば1つの角度が算定できます。 よって、正六角形の1つの角度は「7÷6=1°」です。 また、外角=180°-内角=180-1=60°です。 三角関数の角度を求めるときは、θの範囲を忘れないこと それぞれの求め方をまとめると 単位円 を書いて、三角関数に適した直線を書き込み交点を求める。 交点と原点の間に線を引き、 三角形の比 から角度を求める。 その際に、 θの範囲内にあるかと、上の三角形の内角に集ま ってくるから180°になりま す。 AさんとCさんの考え は、三角形の内角に集まっ ているところが似ていると 思います。 Cさんの考え方は、前に習っ たやじり形を利用して求めてい からも使えそうです。
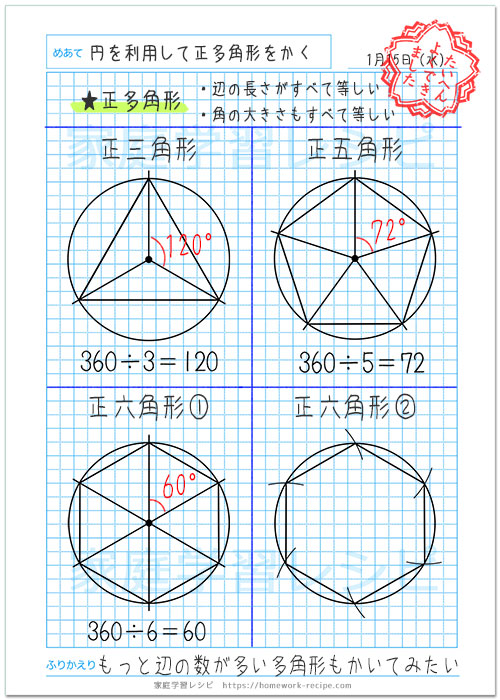
円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ
六角形 角度 求め方
六角形 角度 求め方- 正六角形は対角線で、4つの三角形に分かれるので、内角の和は、 180×(6-2)=7度 正六角形の角は全部で6つあるので、1つの角の大きさは、 7÷6=1度 で求め図形の性質の調べ方 平行線と角(3) 1 次の図で、l mのとき、∠x、∠yの大きさを求めなさい。同じ印をつけた角は それぞれ等しい。 (1) (2) (3) 243 x 70° 115° E x l 40° m x l ° m x l 10° m
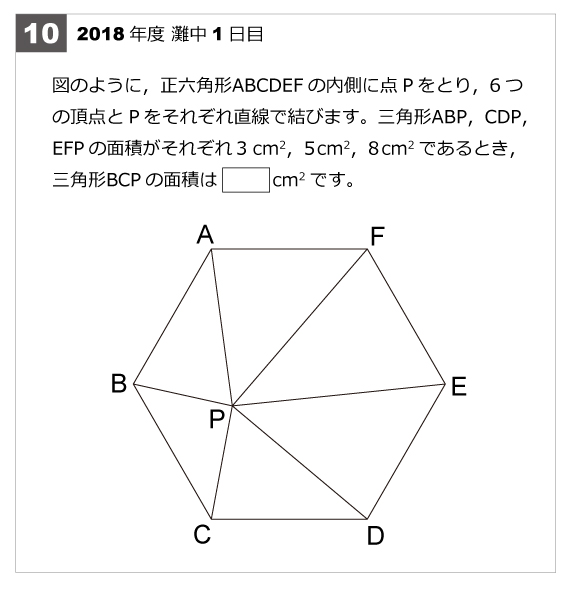



灘中解説速報 18年第10問 正六角形と面積 算数星人のweb問題集 中学受験算数の問題に挑戦
三角形の角度を求める問題 ではこれらの性質を使って、三角形の角度を求める問題を解いていきたいと思います。 問題① 下の図における ∠x の大きさを求めなさい。 三角形の外角の大きさ=となり合わない2つの内角の和 であることから x+60°=135° 多角形(五角形や六角形、十角形など)の 内角の和の求め方について、スマホでもみやすいイラストで簡単に解説 していきます。 多角形の内角の和は、とても簡単に求めることができます。本記事を読めば、一瞬で内角の和が求められるでしょう。 今回は、早稲田大学に通う筆者が、多角形 三角形の3辺の長さから角度を求める 三角形の記号 使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。 角度は、次の2段階のステップで求めます。 求める角度の余弦(cos(コサイン))を求める。
180×(6-2)=180×4=7 正6角形の1つの角の大きさは次の式で求めます。 180-(360/6)=180-60=1 12人 がナイス! 正四角形(正方形)は対角線で三角形2個に分けられるので 正方形の内角の和は180°×2=360° 同じように考えて 正五角形は三角形3個分で180°×3=540° 正六角形は三角形4個分で180°×4=7° 各角の大きさは 正五角形は540°÷5=108° 正六角形は7°÷6=1° 「一辺の角度は何℃か」はわかりませんでした。 36人 がナイス! しています 正六角形 (せいろっかくけい)とは、各辺の長さがすべて等しく、内角も1゚と一定な六角形である。 一辺をaとすれば 周長 は 6 a {\displaystyle 6a\,\!} であり、外接円の直径 (対角長)は 2 a {\displaystyle 2a\,\!} であり、内接円の直径 (対辺の距離)は 3 a {\displaystyle {\sqrt {3}}a\,\!} であり、面積は下記のとおりとなる。 A = 3 2 a 2 cot π 6 = 3 3 2 a 2 ≃ a 2
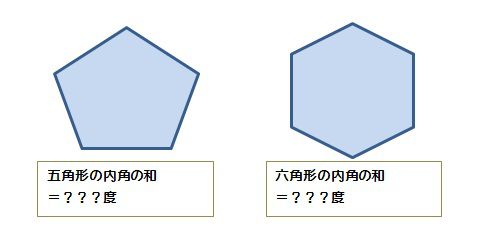
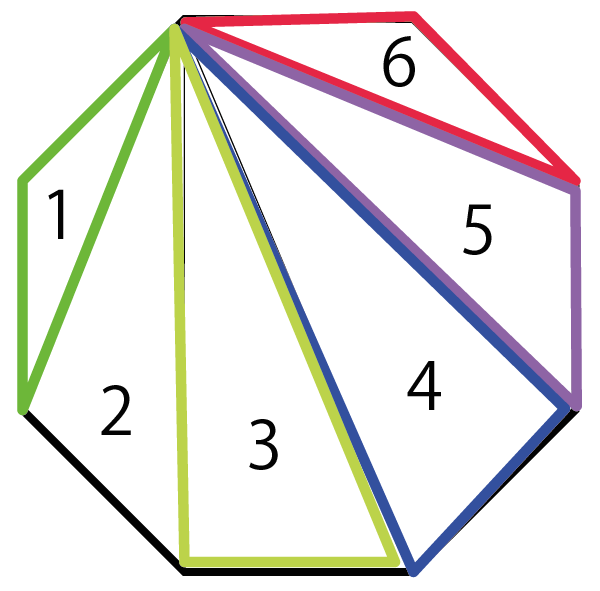
色々な星形多角形を作図し、頂角の和を求めなさい。 どんな求め方がありますか。またいどんなことに気がつきますか。 ・この教材は図形の調べ方の単元の最後に扱う「星形五角形の頂角の和」を、生徒が主体的に取 り組めるように問題作りの形で扱った発展的課題である。 3 数学的な価値 六角形の内角の和を3秒で計算できる公式 多角形の内角の和の公式 を使うだけでOK。 n角形の内角の和って、 180× (n2) で計算できたよね? 今回は、6角形の内角の和を計算したいので、 nに「6」を代入しよう。 すると、六角形の内角の和=180×(6-2)=180×4=7度 10角形の内角の和=180×(10-2)=180×8=1440度 2 正 角形の1つの内角の大きさを求める! 正三角形の1つの内角の大きさは60度 , 正四角形(正方形)の1つの内角の大きさは90度です。 五角形 , 六角形 の1つの内角の大きさを求めてみましょう。 正 角




課題学習の指導 数学



一辺の長さが4cmの正六角形があります この正六角形の面積を求めなさいこの Yahoo 知恵袋
六角形の面積を求める方法 六角形とは多角形の1つで6つの辺と角度に囲まれています。基本の六角形は辺の長さと角度のがすべて均一で、6つの二等辺三角形が合わさった形状をしています。変則的な形状も含め、六角形の面積を計算する方法は複数あります。下記の方法を参考に計算方法を学びましょう。 辺の長さが分かっている時は公式を用いる 基本の六角形は6三角定規の角度や分度器や直線定規の数字を使う描き方(作図ではない)を1つ。 正六角形は亀甲、籠目、麻の葉などの幾何学模様や連続模様の基本となります。 正六角形の条件 ・6辺の長さが等しい。 ・6個の内角がそれぞれ等しく1度(六角形の内角の和は7度)。 コンパスと定規を使ったおもしろ自由研究 5 星形の角の和の求め方 2番目 ごと 1番目 ごと 2番目ごと に結んだ星 形五角形と 同じになる。 2番目ごと に結んだ星 形六角形と 同じになる。 3番目ごと に結んだ星 形七角形と 同じになる。 3番目 ごと かくことが できない。 かくことが できない。 4番目




辺の長さの異なる六角形の面積 辺の長さの異なる六角形の面積 向き合う辺 Okwave



小学生算数正六角形の角度を求める問題 詳しい説明でお願いします Yahoo 知恵袋
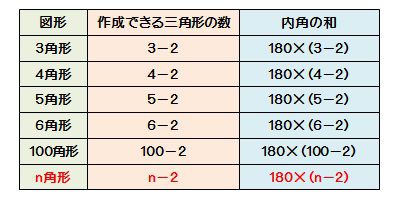
四角形の内角の和: 360° 360 ° 五角形の内角の和: 540° 540 ° 六角形の内角の和: 7° 7 ° ・・・ n角形の内角の和: 180°× (n−2) 180 ° × ( n − 2 ) この公式は覚えやすいので暗記してもいいのですが、簡単に導出できるため、わざわざ覚える必要もありません。 ではどのようにこの公式を導出するのか、なぜ内角の和が「 180°× (n −2) 180 ° × ( n1 コンパスを使って円を描きましょう。 コンパスに鉛筆を装着し、描く円の半径に合わせてコンパスを適当な幅に拡げます。 5~8センチ程度の幅で結構です。 次に、コンパスの針を紙面上に固定して、円ができるまでコンパスを回します。 まず一方向に半円を描いた後に、逆方向に戻って逆向きにもう一方の円を描く方が楽なこともあります。 {"smallUrl""https・星形六角形の頂角の和は,ほとんどの生徒が求めている。 <発表された生徒の解き方> (4) レポート作成の課題を与える。 1) 頂角の和が180度になる星形多角形を調べよう。 2) 星形偶数多角形の性
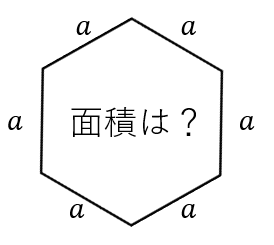



正六角形の面積 計算ツール 公式の導出 具体例で学ぶ数学



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
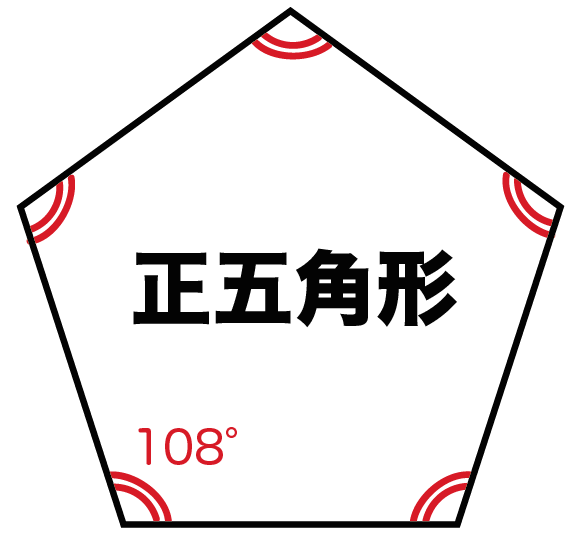
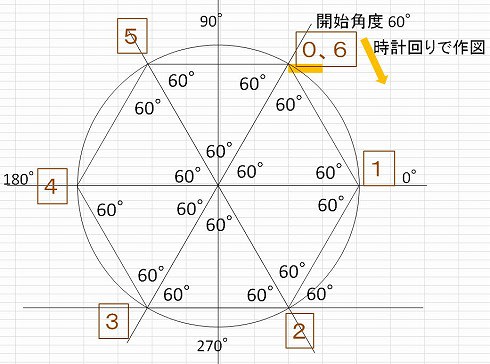
円を使った正多角形のかき方を考えさせ、動画で確かめさせます。 円を使った正六角形のかき方 円中心のまわりを6等分して、 60度になるように分度器で 半径を順にかきます ※分度器の使い方 ↓ 次にそのはしの点を直線でつなぐと 正六角形ができます。 外角・内角の和、面積、対角線の本数の公式と求め方 21年2月19日 この記事では、「多角形」の種々の公式(外角の和・内角の和、面積、対角線の本数など)やその求め方をわかりやすく解説していきます。 また計算問題の解き方もわかりやすく解説して 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180× (52)/5 = 108°




多角形の内角の和 算数の公式覚えてますか




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト
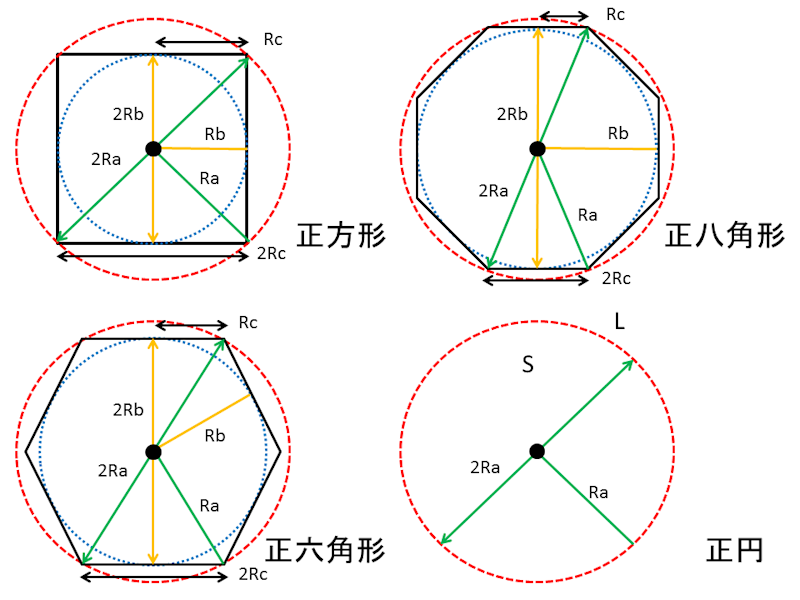
正多角形の内角・外角の求め方を解説! 星形の角度の求め方を解説!←今回の記事 ブーメラン型の角度の求め方! ちょうちょ型の角度の求め方を解説! 合同な図形の基本性質とは? 三角形の合同条件を使って、合同な三角形を見つける方法!図形の面積の求め方(公式ほか) 正方形・円・長方形・平行四辺形・三角形・扇形・楕円・台形・双曲線・放物線・六角形・多角形 光正株式会社 役立つ資料シリーズ 図形の面積の求め方 A=面積 A=s 2 A=1/2d 2 S= d= d=1414 s=1414 A=面積 =弧の長さ a=角度 A=面積 A=面積 =弧の長さ a=角度 円の周りを半径の長さで区切る方法で正六角形をかき、その方法でかける理由を考える。 直径と円周の長さの関係について見通しをもって調べようとしている。 5 6 円周率の意味や求め方を理解し、円周の長さを求めることができる。



720度 星形九角形の角度の和



正多角形の1つの内角 外角を求める方法を問題解説 数スタ
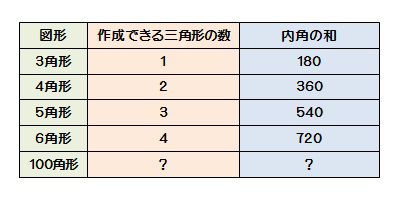
大体のやり方は分かってもらえたでしょうか?? とにかく、360°から角の数だけ割ってやれば1つ分を出すことができますね! 正六角形の外角は\(360 \div 6 =60°\) 正八角形の外角は\(360 \div 8=45°\) 正九角形の外角は\(360 \div 9=40°\) 正十角形の外角は\(360 \div 10=36°\)・その内部に作成できる三角形の数:(n-2)個 という意味です。 試しに数値を代入して確認してみましょう。 ・五角形の場合:n=5 ・内部に作成できる三角形の数:n-2=5-2=3個 540度 どうですか?五角形の内角の和は540度で間違いないですよね?教え方3 教え方3-① 円周と直径の意味を教え、円周の長さと直径の長さの関係を調べさせ、円周率を理解させます。 直径は、半径の2倍の長さです 円の周(まわ)りを円周といいます 直径10cmの円をかいて、調べます 直径10cmの中に正六角形をかくと
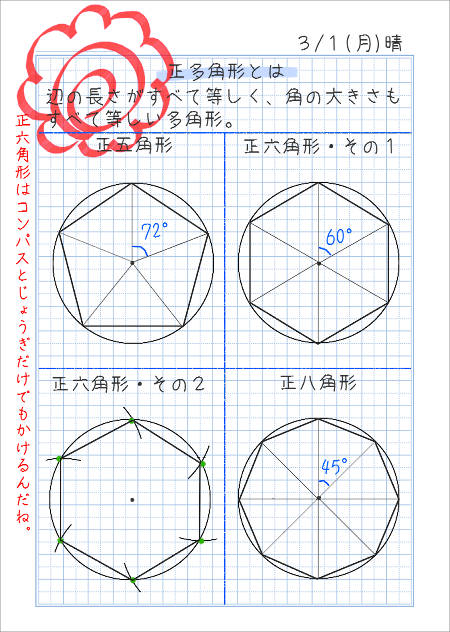



いろいろな正多角形をかいてみよう 家庭学習レシピ
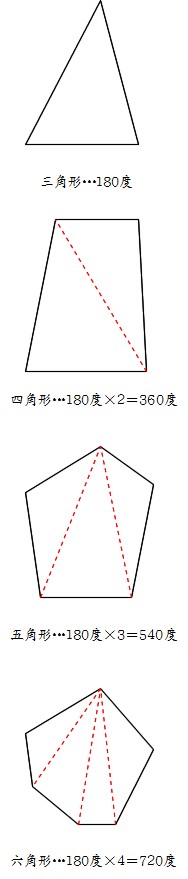



Math 多角形の内角の和 働きアリ
Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos θ = a c , sin θ = b c , tan θ = b a ( 2)*ここでの別名・英語名・中国語名共に一般的な名称ですが、使われ方が違う場合もありますのでご注意下さい。 六角ナットの特徴 六角ナットに限らずナット類はボルト類や小ねじ類と組み合わせて、二つ以上のものを固定する為に使用され、単独で使用される事はありません。 その中でもこ�左から「三角形」「四角形」「五角形」です。 また、図形の内側の角を 内角 といい、それから延長した辺と1辺がつくる角を 外角 といいます。 この2つの角度を足すと 180° になります。




小5 算数 小5 33 五角形 六角形 多角形 Youtube




数学 中2 51 多角形の内角と外角の和 基本編 Youtube
Jw_cad (JWW) ではじめてCAD作図するかたに、多角形、文字、寸法線の作図パターンの基本を説明、多様な機能を搭載した汎用2DCAD、Jw_cad (JWW)の入門の手助けとなります。星型多角形とは,一般的な多角形とは異なり特 殊な形をしているが,見方を変えることで両者の 関係性が明らかになった。 (4) 星型多角形の内角の和の求め方 ることは,多角形を三角形に分割することで演繹 的に示すことができる。では,星型多角形も同様
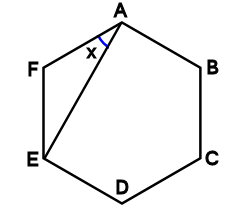



正五角形の中の角度



1
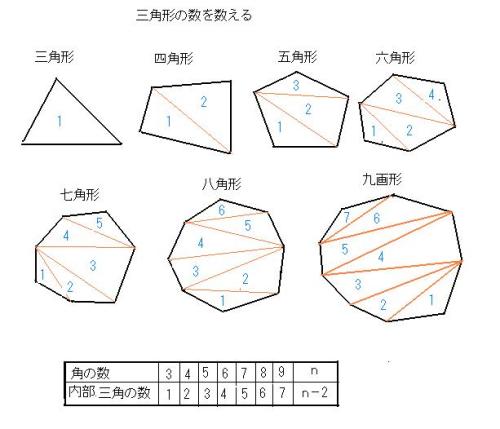



多角形の内角の和を簡単に求める方法 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ



正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ
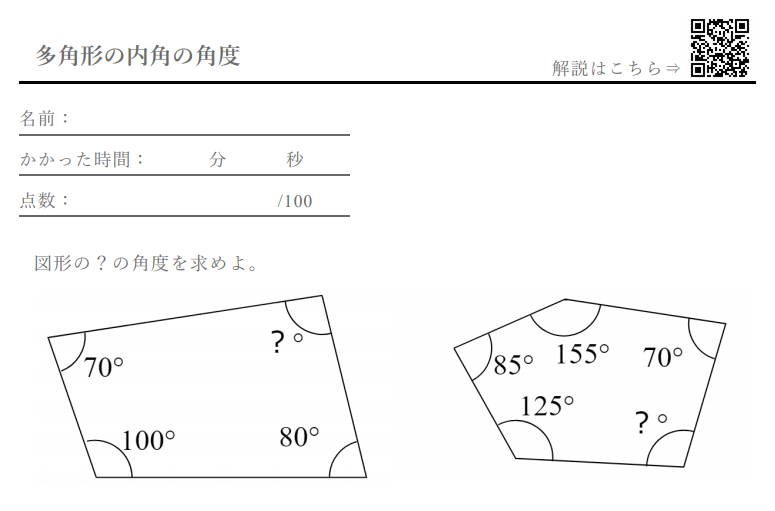



多角形 の内角の角度 計算ドリル 問題集 数学fun
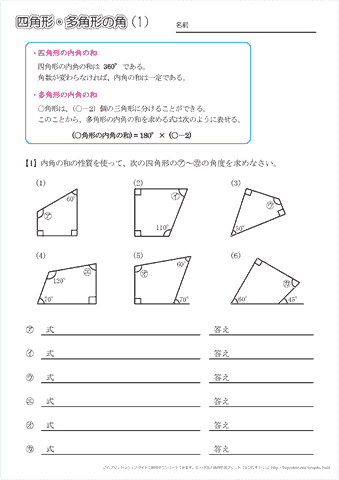



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




灘中解説速報 18年第10問 正六角形と面積 算数星人のweb問題集 中学受験算数の問題に挑戦
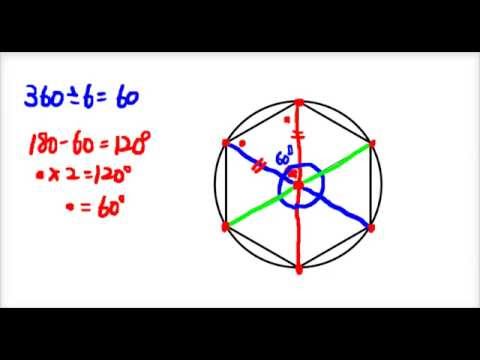



簡単にわかる 正六角形のかきかた ふるやまんの算数塾 Youtube




正多角形の1つの内角 外角を求める方法を問題解説 数スタ



サッカーボールの型紙 エクセルvbaで正六角形を作図しますpart 2 日だまりのエクセルと蝉しぐれ



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note




円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ
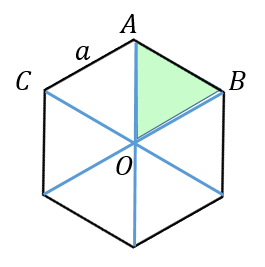



正六角形の面積 計算ツール 公式の導出 具体例で学ぶ数学




内角の和 180 N 2 外角の和 360 教遊者



すべての内角が1度である六角形 思考力を鍛える数学




正多角形をプログラムを使ってかこう 杉並区立西田小学校 未来の学びコンソーシアム



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




多角形の内角の和 は何度なのか を説明します おかわりドリル




小学校5年 算数 正多角形の角の大きさ Youtube



正8角形 正八角形 の角度の求め方は 1分でわかる内角の和 計算 外角 正9角形の角度




中2数学 六角形の内角の和が3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
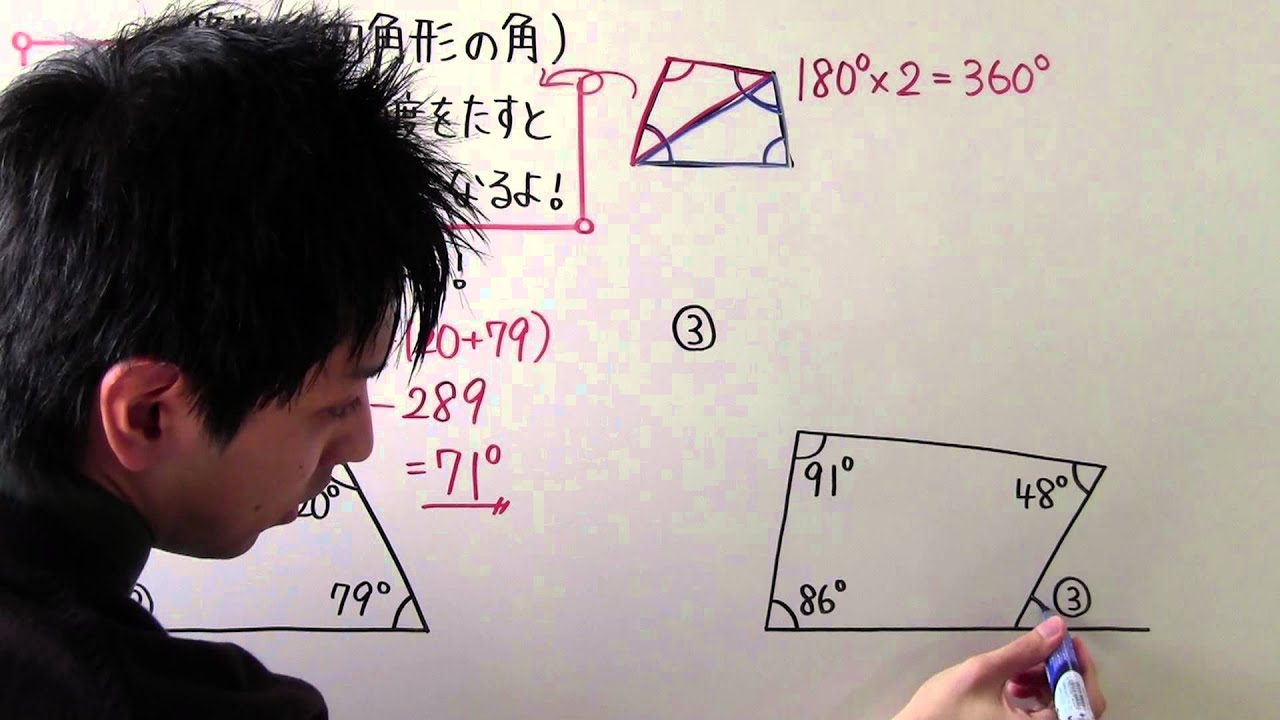



小5 算数 小5 32 四角形の角 Youtube




多角形の内角の和 外角の和の公式 数学fun



正六角形の合計の角度と一つの角度の求め方を教えてください 公式とかも教 Yahoo 知恵袋
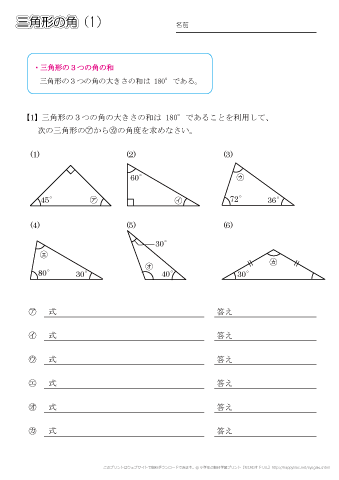



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



720度 星形九角形の角度の和
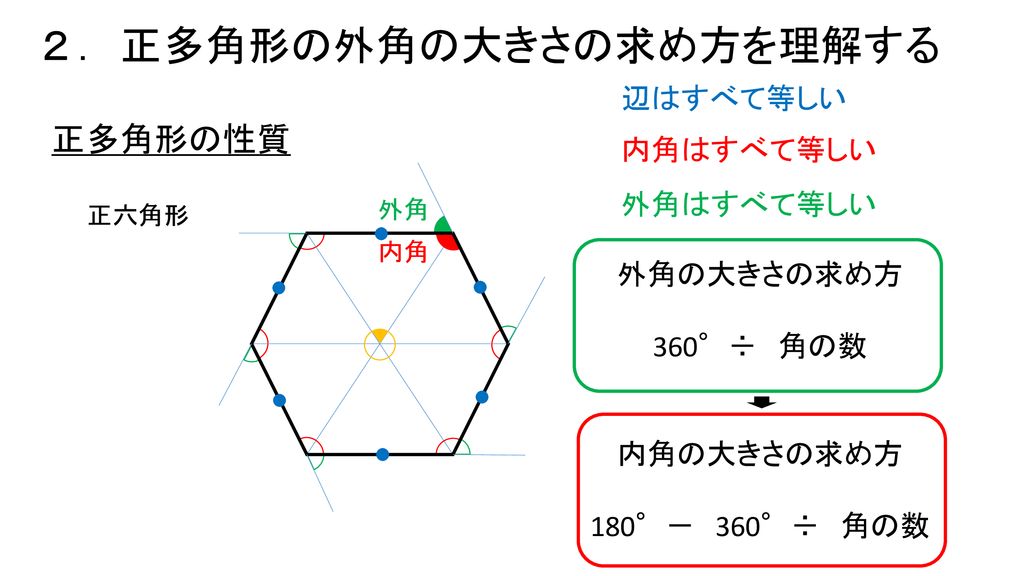



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download



正5角形の角度の求め方は 1分でわかる値 内角の和 正6角形 正8角形の角度は
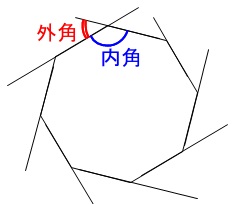



多角形の内角の和の公式と外角の和を利用した角度の求め方



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫
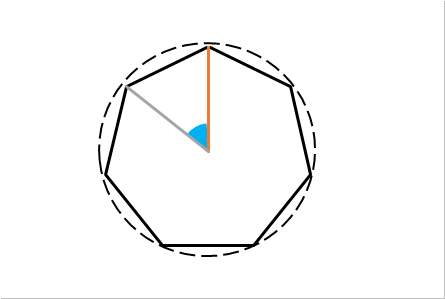



小5 B いろいろな図形 多角形



多角形の内角の和 算数の公式覚えてますか
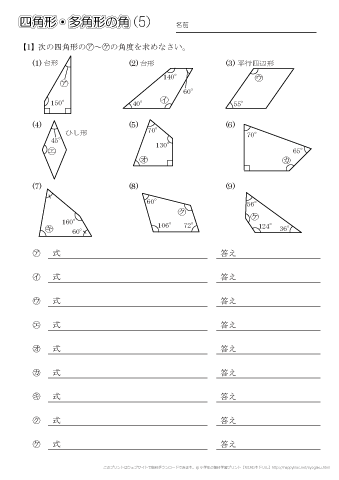



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生



720度 星形九角形の角度の和




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
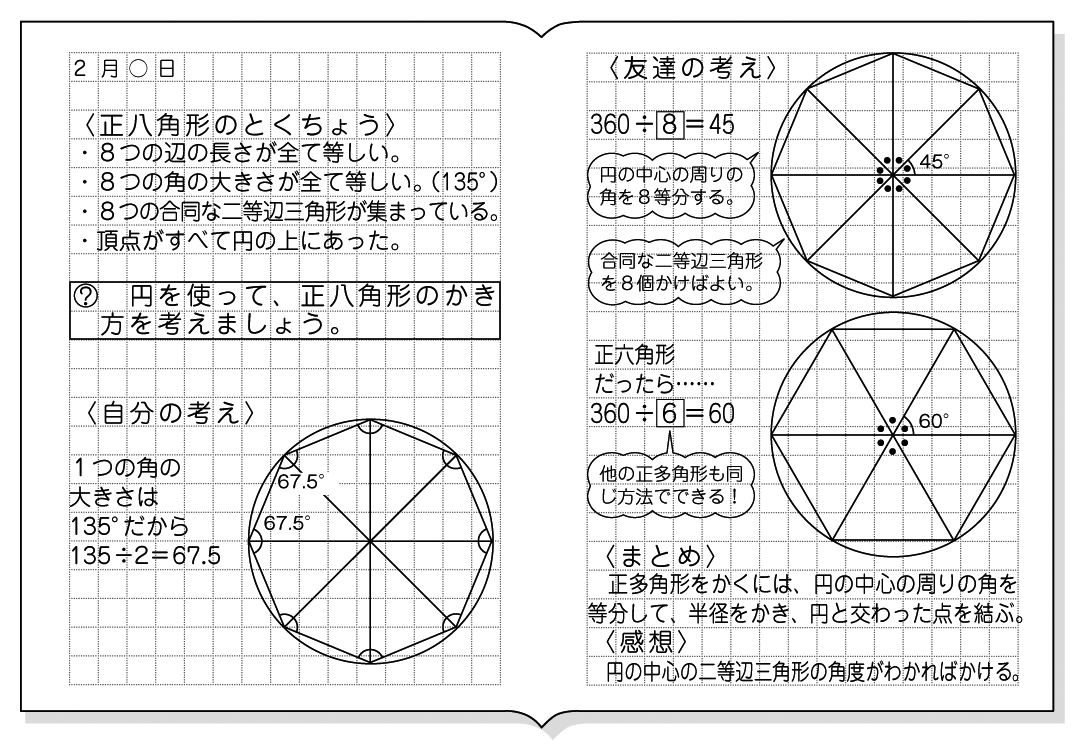



小5算数 正多角形と円 指導アイデア みんなの教育技術




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
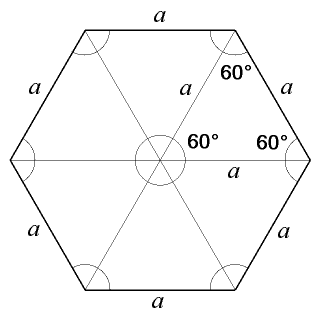



正六角形 ゆるゆるプログラミング



多角形の内角の和 算数の公式覚えてますか




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題
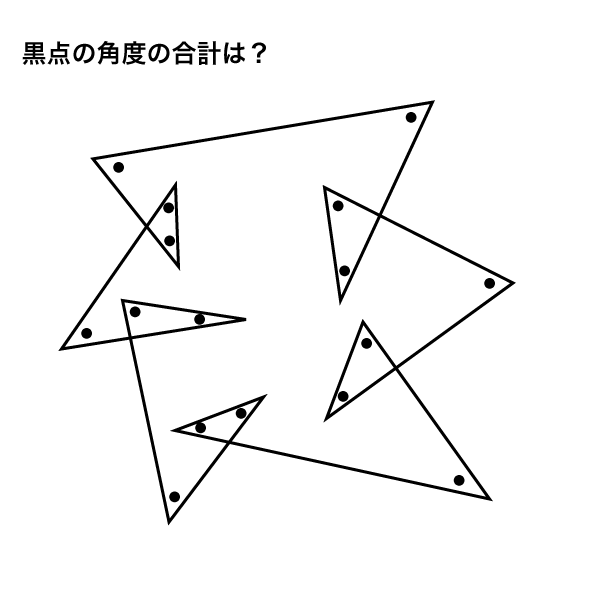



角度情報がない図形の合計の角度 星形多角形 受験算数入門



1




多角形の内角の和の公式と外角の和を利用した角度の求め方
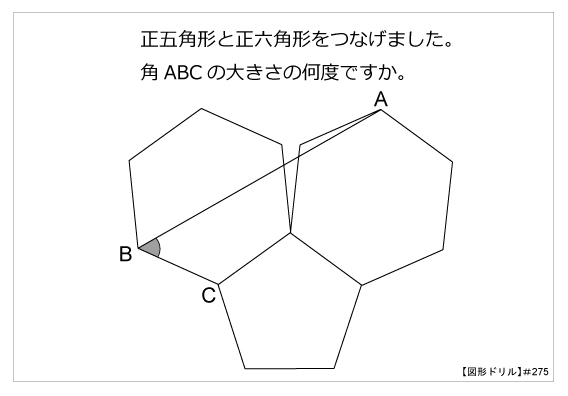



図形ドリル 第275問 正五角形と正六角形 算数星人のweb問題集 中学受験算数の問題に挑戦




多角形の内角の和 算数の公式覚えてますか




六角形鏡加工について アンティークミラー Com



多角形の内角の和 算数の公式覚えてますか




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




正十八角形の1つの内角の大きさを求めなさい この問題の解き方教えてください Clear




内角の和 180 N 2 外角の和 360 教遊者



3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく




六角形鏡加工について アンティークミラー Com
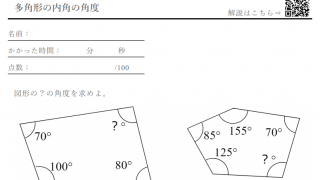



多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




11 号 多角形型太陽電池モジュール Astamuse
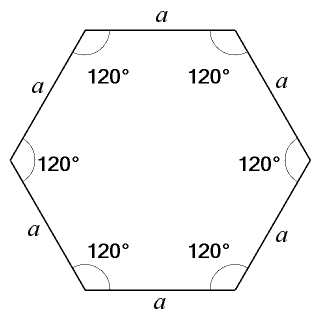



正六角形 ゆるゆるプログラミング




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ
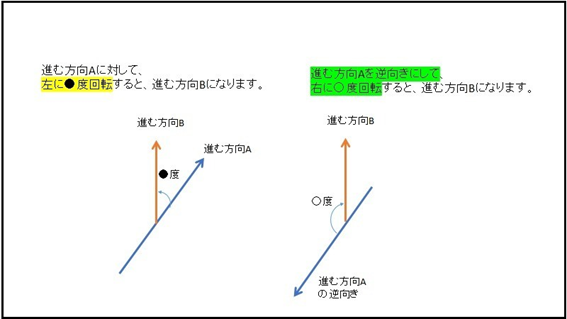



小5算数 内角の大きさを求めて正多角形を作図しよう ベネッセのプログラミング教育情報



すべての内角が1度である六角形 思考力を鍛える数学



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
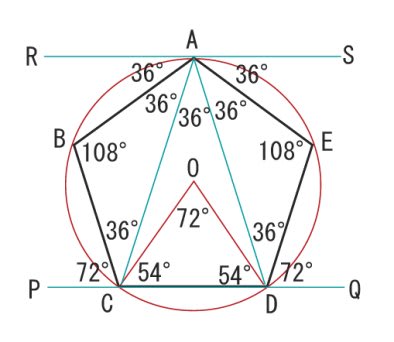



正五角形というだけで 分かる角度は 名寄 算数数学教室より




多角形の内角の和 は何度なのか を説明します おかわりドリル




中2 数学 図形の性質5 多角形の内角 6分 Youtube
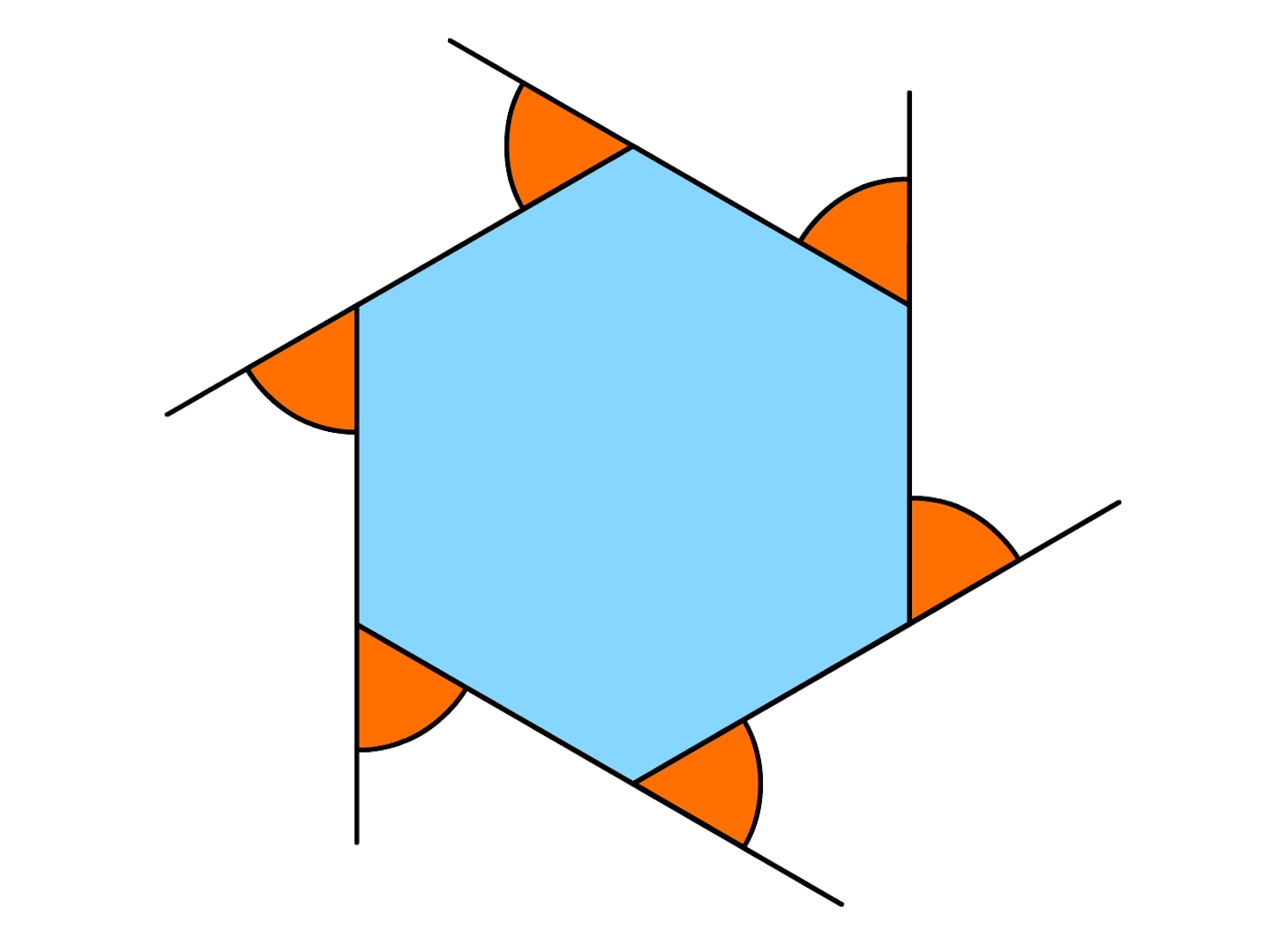



2年 多角形の外角 数学イメージ動画集 大日本図書




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




正六角形角度 平面図形の角度 Lousi Imagine




Cube Taraognn




中2数学 複雑な多角形 角の和 応用問題




中2数学 六角形の内角の和が3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



コンパスと定規を使った正六角形の描き方 図形の描き方012a 夏貸文庫




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より




小5 算数 小5 54 正多角形 Youtube



Q Tbn And9gctqxnxegjdxp Adpruavnpmf2sansioyhqkmwlqdbcw Fiiw67x Usqp Cau
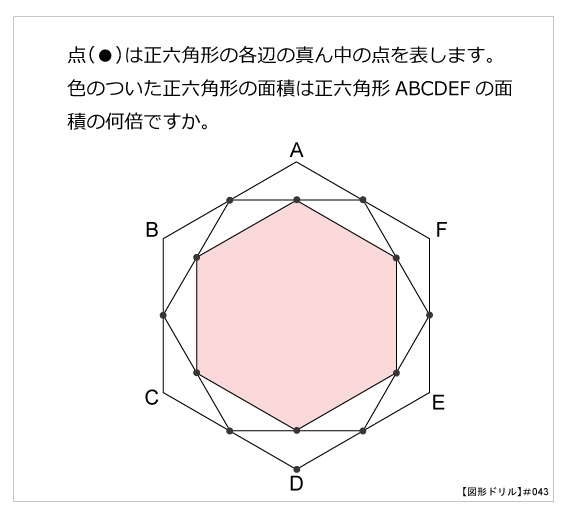



図形ドリル 第43問 内接する正六角形 算数星人のweb問題集 中学受験算数の問題に挑戦




内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学




六角形 Wikipedia
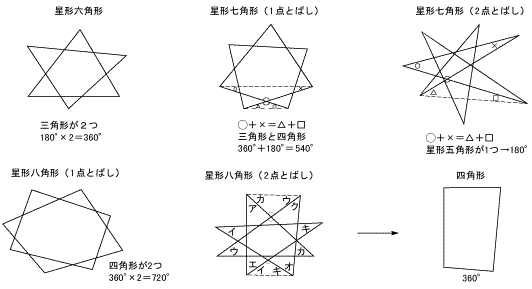



課題学習の指導 数学



正六角形 どう解く 中学受験算数



3




中2数学 六角形の内角の和が3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



正多角形 Color Cube ウィキ Atwiki アットウィキ



0 件のコメント:
コメントを投稿